
Este obra está bajo una licencia Creative Commons Atribución 3.0 Ecuador.
Antecedentes
Voy a tomar como base un artículo "Una curiosa propiedad del 123" de la página: Una curiosa propiedad del 123, cuyo texto reproduzco a continuación.
Una curiosa propiedad del 123
Me gustan esos números que “atraen” a otros números después de realizarles a estos últimos ciertas operaciones. Esos números que, casi como por arte de magia, salen siempre como resultado de dichos cálculos. Números como el 6174 (la constante de Kaprekar para números de cuatro cifras) o el 1089. Me encantan estos números, a los que cariñosamente llamo agujeros negros por tragarse a esas cantidades de números y no dejarlos escapar.Hoy os voy a mostrar una curiosa propiedad del número 123 que lo convierte en uno de esos agujeros negros numéricos y que, por qué no, podría servir para introducir a alumnos de secundaria en el maravilloso (pero complicado) mundo de las demostraciones matemáticas.
La propiedad del 123 a la que me refiero es la siguiente:
Tomamos un número entero positivo cualquiera de tres o más cifras y contamos cuántas de ellas son pares y cuantas impares, y con estos datos construimos un número de la siguiente forma: colocamos primero la cantidad de cifras pares que tenía el inicial, después la cantidad de cifras impares y después la cantidad total de cifras que tenía. Con el número obtenido hacemos lo mismo, y así sucesivamente. Sea cual sea el número inicial siempre terminaremos en el 123, y no saldremos de él.Vamos a ver un ejemplo. Tomamos, por decir alguno, el 863112. Tiene 3 cifras pares (el 8, el 6 y el 2) y 3 impares (el 3, el 1 y el 1). Como tiene 6 cifras, con él obtendríamos el número 336. Hacemos lo mismo con éste: 1 dígito par (6) y 2 impares (3 y 3). Como tiene 3 cifras, obtenemos con él el 123. Y ahora el 123 tiene una par (el 2), dos impares (el 1 y el 3) y tres dígitos, obteniendo así el número 123 de nuevo. Por tanto el 123 se ha tragado al 863112 cual agujero negro.
Curiosa a la par que enigmática propiedad del 123, ¿verdad? No sé si os ha sorprendido, o si os parece muy compleja o más bien trivial. La cuestión es que es bastante sencillo demostrarla, y pienso, como ya he dicho, que la prueba de esta propiedad podría servir para introducir en el magnífico a la vez que complejo mundo de las demostraciones a los alumnos que todavía no están muy familiarizados con ellas. Vamos a verla:
Si el número tiene 3 cifras puede pasar varias cosas:Por poner un ejemplo con un número grande, tomemos uno de 63 cifras:
- Que las tres sean pares: entonces tendremos 0 impares, con lo que obtendríamos el 303. Éste tiene una par y dos impares, con lo que, por tener tres cifras, llegamos al 123.
- Que las tres sean impares: tendremos ahora 0 pares, con lo que tendríamos el número 033. Volvemos a tener una par (recordad que el cero es un número par) y dos impares, llegando igual que antes al 123.
- Que haya dos pares y una impar: obtendríamos de él el 213. Dicho número tiene una par y dos impares, con lo que llegaríamos de nuevo al 123.
- Que haya dos impares y una par: en este caso nos sale directamente el 123.
Si el número tiene 4 cifras o más, llegaremos siempre a un número de 3 cifras después de aplicar este proceso una cierta cantidad de veces. Cuando se llegue a ese punto se utiliza lo que hemos comentado antes y volvemos a llegar, siempre, al 123.
En consecuencia, esta propiedad del 123 es cierta sea cual sea el número entero positivo de tres o más cifras con el que comencemos.
No me podréis negar que la demostración es bien fácil, ¿verdad? La magia de las matemáticas apta para todos los públicos.
Fin el artículo aparecido en la página.
Mi conclusión y aporte
No hay que negar que resulta ingenioso este descubrimiento, pero los ejemplos que pone no son, ni mucho menos, una comprobación y esto puede llevar a errores en el sentido que el lector puede inferir que unos cuantos ejemplos sirven como "comprobación". La comprobación debe abarcar todos el universo de números que se quiere involucrar, pero basta con conseguir un solo ejemplo para el cual no funcione para desechar la propiedad. Como me fue dificil conseguir un solo ejemplo para el cual no funcione la propiedad, me di a la tarea de comprobar esta propiedad para todo número, lo cual comparto con ustedes, en esta magia de las matemáticas.
Demostración:
Todo número, es convertible a uno de tres cifras por ejemplo N = 12345678900987654321, tiene longitud 20, con 10 cifras pares y 10 cifras impares y por tanto se convierte en (10) (10) (20), que se descompone nuevamente en 426. Por tanto esta demostración tiene como punto de partida un número de 3 cifras.
Entonces la condición previa es que todo número se ha convertido en uno de 3 cifras o dígitos nnn
Entonces todo número cuya cantidad de cifras impares es impar y la cantidad de cifras pares es impar se convierte en 123.
Entonces todo número cuya cantidad de cifras impares es par y la cantidad de cifras pares es impar se convierte en 123.
Entonces todo número cuya cantidad de cifras impares es impar y la cantidad de cifras pares es par se convierte en 123.
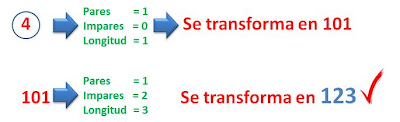
Queda por comprobar los diez números de longitud 1.
para los número 5, 6, 7 ,8, 9 & 0 el procedimiento es similar.
Queda por comprobar los número en el rango [10,99] cuya técnica es igual a la anterior o se pueden trabajar como: 010, 011, 012, ... ,099 números de tres cifras.
La propiedad también es extensiva para los negativos. En general para todo el conjunto de los enteros {Z}.








Gracias por tomarte este ejercicio con ese gran interes por decifrar que siempre te ha caracterizado...Ademas, la explicacion es nitida y nitidamente presentada...Este es el Bolivar que siemore conoci, socratiano, emprendedor con fuerza a la cervantina, y no recuerdo ningun fracaso en su vida y si recuerdo que perder era temporal y se levantaba mas airoso y seguro con su lema: siempre pa'lante...Tus colegas te admiramos mucho en aquel entonces, y hoy estariamos felices de apoyarte en tus empresas que ya no se ocupan de ti mismo como de dejar un legado honroso y util...como es ensenhar, abrir los ojos, buscar la felicidad mas dando que recibiendo...suerte haberte conocido y tus consejos siempre sabios por la propia experiencia tuya aun continuo aplicando...desde querecual ;)
ResponderEliminarHola hermano
EliminarTengo solo unos tres amigos con las características del pensamiento (casi dos). Gracias por escribirme. En este momento estoy lejísimos, en La Paz haciendo Veedurá Popular al proceso eleccionario, invitado por el Gobierno Boliviano
Gracias por tus conceptos. Por favor entra a www.maestromate.blogspot.com, donde tengo un emprendimiento académico para todo el mundo sin condiciones.
Un abrazo solidario.
Aquí en Ecuador soy conocido como el SuperCuy